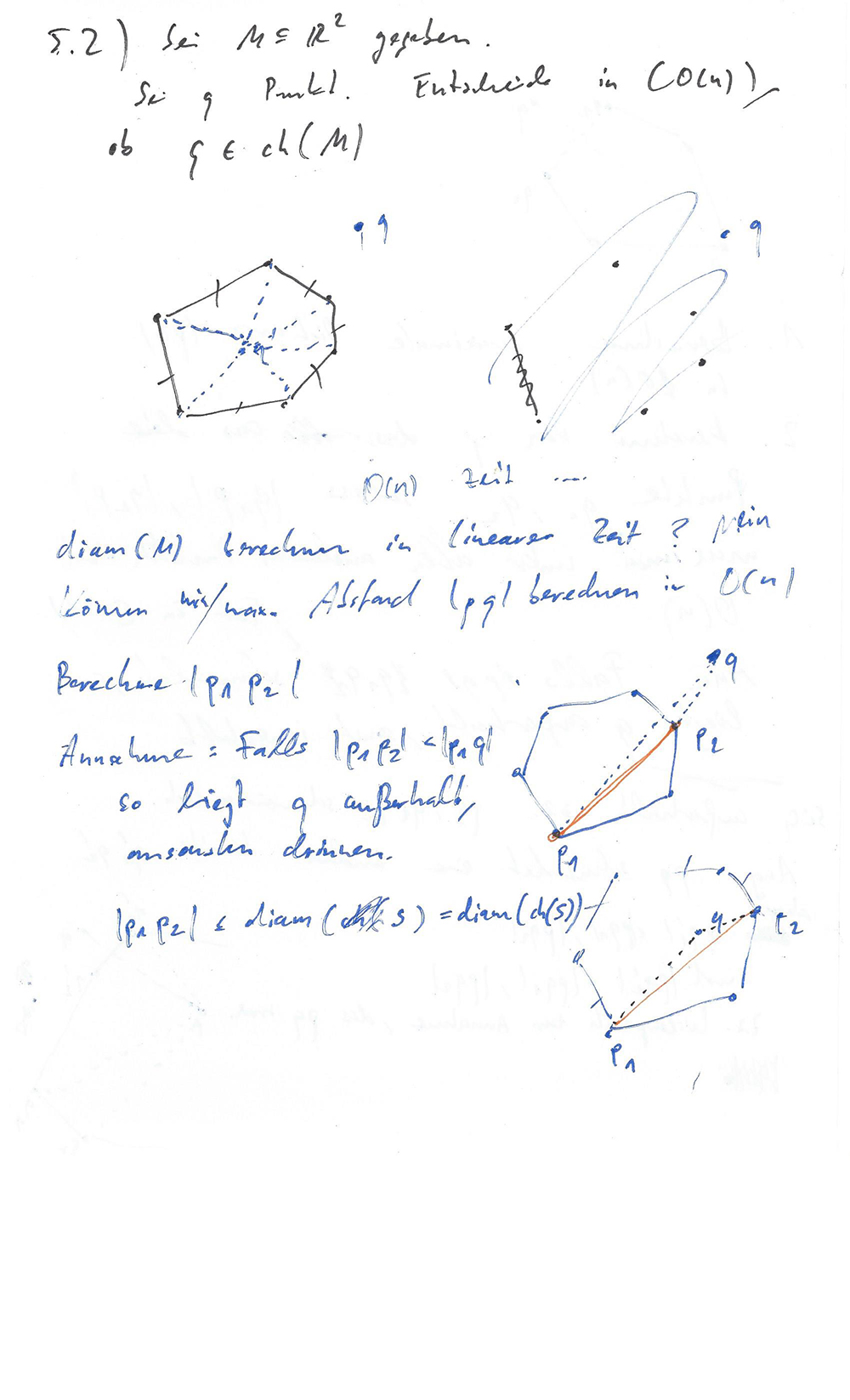
Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 1)

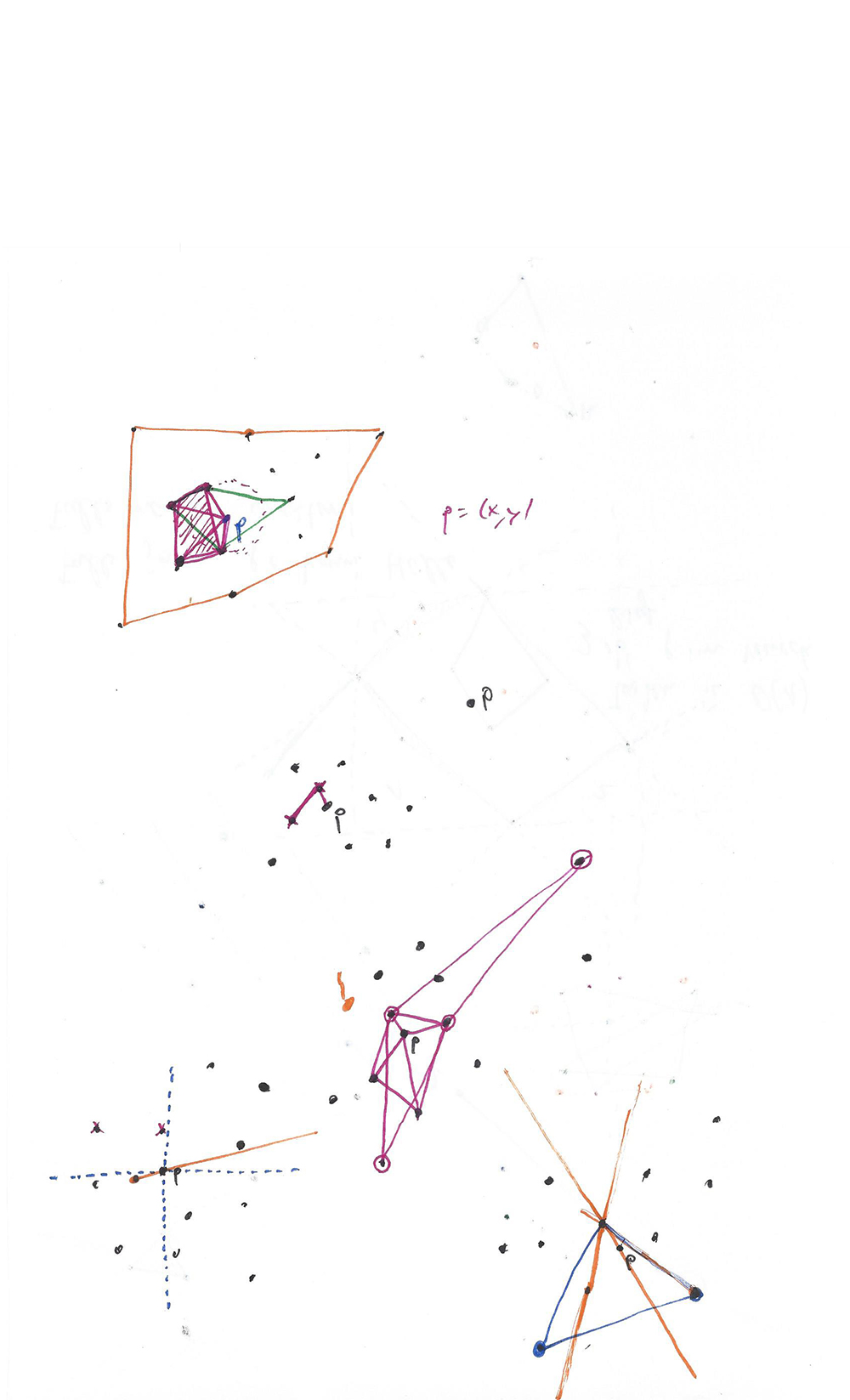
Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 2)

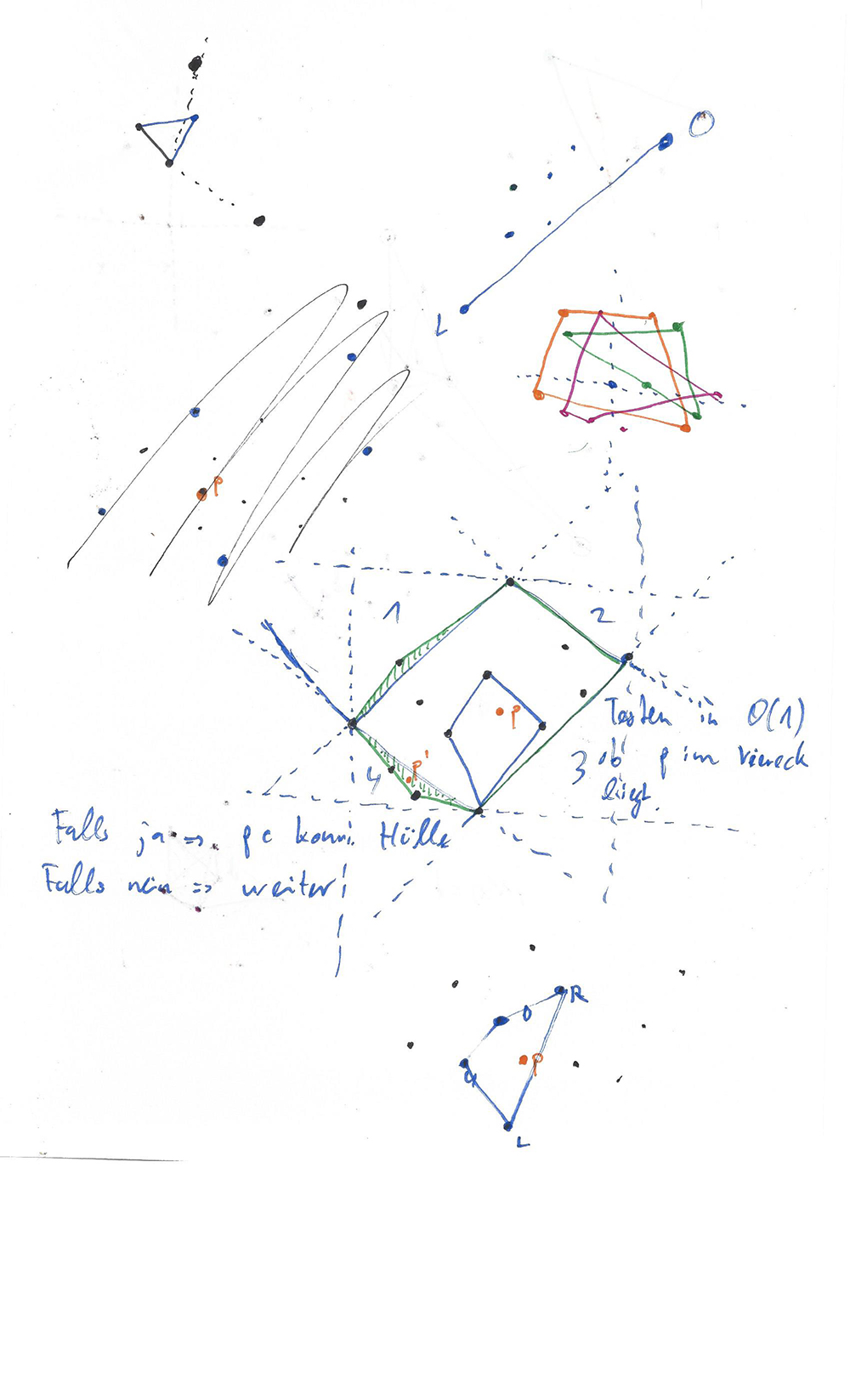
Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 3)

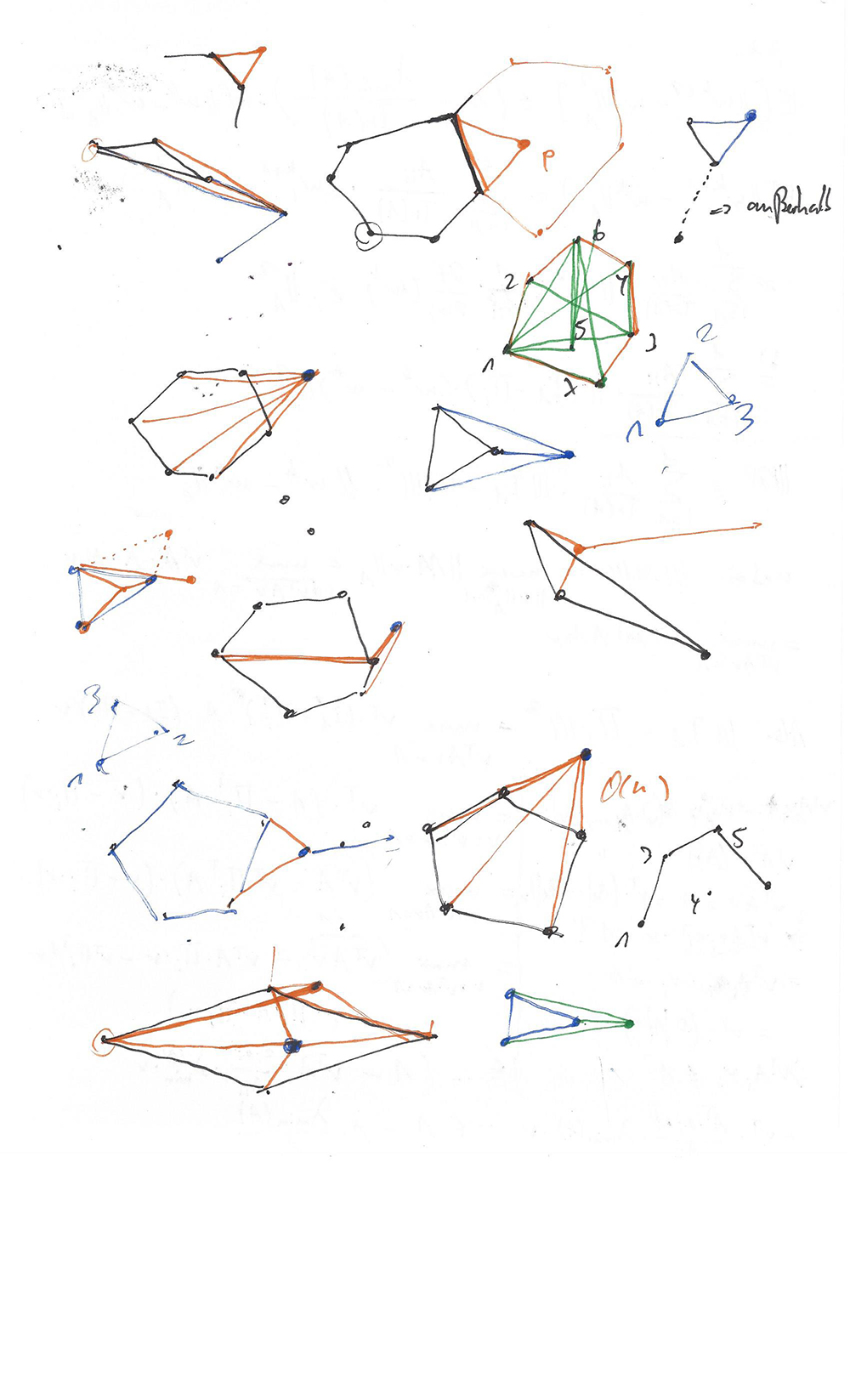
Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 4)

Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 5)

Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 6)

Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 7)

Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 8)

Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 9)

Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 10)

Solution process of a problem in computational geometry.
Im Lösungsprozess eines mathematischen Problems spiegelt sich das Wesen des Lebens wieder: Die Irrpfade und Sackgassen, die beim Lösen von Problemen aufkommen, bilden die Grundlage, ohne die Wachstum nicht möglich wäre. Ohne und Verwicklungen/Verwirrungen entstehen keine Entwicklungen/ Entwirrungen. (Seite 11)

Solution process of a problem in computational geometry.
Seite mit der Lösungsskizze. (Seite 12)